(data structure)
Definition:
(1) A data structure accessed beginning at the root node. Each node is either a leaf or an internal node. An internal node has one or more child nodes and is called the parent of its child nodes. All children of the same node are siblings. Contrary to a physical tree, the root is usually depicted at the top of the structure, and the leaves are depicted at the bottom. (2) A connected, undirected, acyclic graph. It is rooted and ordered unless otherwise specified.
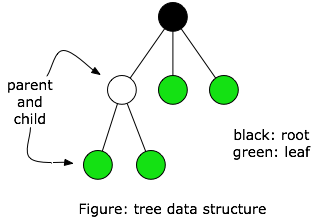
Thanks to Joshua O'Madadhain ([email protected]) for the figure, 6 October 2005.
Formal Definition: (1) A tree is either
Specialization (... is a kind of me.)
heap, B-tree, binary tree, balanced tree, multiway tree, complete tree, search tree, digital tree, Merkle tree.
See also other vocabulary: descendant, ancestor, tree traversal, height, depth, degree (3), technical terms: ordered tree, rooted tree, free tree, arborescence.
Note: Appearing in the Dictionary of Computer Science, Engineering and Technology, Copyright © 2000 CRC Press LLC.
A tree in the data structure sense (1) is not the same as a tree in the graph sense (2). Consider possible binary trees with two nodes. There are two possible data structures: a root and a left subtree or a root and a right subtree. However there is only one possible graph: a root and a subtree. The graph definition doesn't allow for "the subtree is the right subtree and the left subtree is empty". Also there is no "empty" graph tree.
Thanks to Sharat Chandran ([email protected]) for clarifying the difference between these two senses.
The formal definition is after [CLR90, page 94].
If you have suggestions, corrections, or comments, please get in touch with Paul Black.
Entry modified 15 December 2017.
HTML page formatted Wed Oct 30 12:15:31 2024.
Cite this as:
Paul E. Black and Algorithms and Theory of Computation Handbook, CRC Press LLC, 1999, "tree", in
Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. 15 December 2017. (accessed TODAY)
Available from: https://www.nist.gov/dads/HTML/tree.html