Θ

(definition)

Definition: A theoretical measure of the execution of an algorithm, usually the time or memory needed, given the problem size n, which is usually the number of items. Informally, saying some equation f(n) = Θ (g(n)) means it is within a constant multiple of g(n). The equation is read, "f of n is theta g of n".

Formal Definition: f(n) = Θ (g(n)) means there are positive constants c₁, c₂, and k, such that 0 ≤ c₁g(n) ≤ f(n) ≤ c₂g(n) for all n ≥ k. The values of c₁, c₂, and k must be fixed for the function f and must not depend on n.
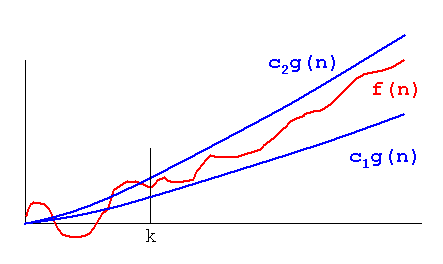
graph showing relation between a function, f, and the limit function, g

Also known as asymptotically tight bound, theta.

Generalization (I am a kind of ...)
big-O notation.

See also ∼.

Note: This is the upper-case Greek letter Theta.

Author: PEB

More information

Donald E. Knuth, Big Omicron and Big Omega and Big Theta, SIGACT News, 8(2):18-24, April-June 1976.

Go to the Dictionary of Algorithms and Data Structures home page.

If you have suggestions, corrections, or comments, please get in touch with Paul Black.

Entry modified 24 February 2016.
HTML page formatted Wed Mar 13 12:42:45 2019.

Cite this as:
Paul E. Black, "Θ", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. 24 February 2016. (accessed TODAY) Available from: https://www.nist.gov/dads/HTML/theta.html