(definition)
Definition: A theoretical measure of the execution of an algorithm, usually the time or memory needed, given the problem size n, which is usually the number of items. Informally, saying some equation f(n) = Ω (g(n)) means it is more than some constant multiple of g(n).
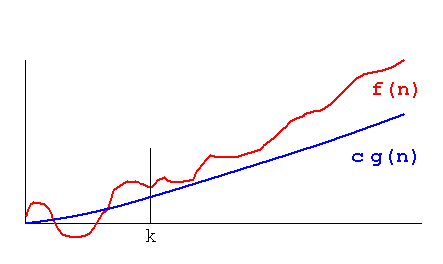
Formal Definition: f(n) = Ω (g(n)) means there are positive constants c and k, such that 0 ≤ cg(n) ≤ f(n) for all n ≥ k. The values of c and k must be fixed for the function f and must not depend on n.
Generalization (I am a kind of ...)
big-O notation.
See also ω(n).
Note: This is the upper-case Greek letter Omega.
This definition is stronger than the traditional mathematical definition. Here, f must be greater than g FOR ALL x bigger than some k. The traditional definition is f is big omega of g if it is not little o of g. That is, one needs only an unbounded sequence of values of x tending to infinity such that cg(x) ≤ f(x) for all x in the sequence.
After Duncan Buell ([email protected]) 21 May 2004.
Author: PEB
Donald E. Knuth, Big Omicron and Big Omega and Big Theta, SIGACT News, 8(2):18-24, April-June 1976.
If you have suggestions, corrections, or comments, please get in touch with Paul Black.
Entry modified 5 March 2018.
HTML page formatted Wed Oct 30 12:15:30 2024.
Cite this as:
Paul E. Black, "Ω", in
Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. 5 March 2018. (accessed TODAY)
Available from: https://www.nist.gov/dads/HTML/omegaCapital.html