knapsack problem

(classic problem)

Definition: Given items of different values and volumes, find the most valuable set of items that fit in a knapsack of fixed volume.

Formal Definition: There is a knapsack of capacity c > 0 and N items. Each item has value v_i > 0 and weight w_i > 0. Find the selection of items (δ_i = 1 if selected, 0 if not) that fit, ∑_i=1^N δ_iw_i ≤ c, and the total value, ∑_i=1^N δ_iv_i, is maximized.

Also known as 0-1 knapsack problem, binary knapsack problem.

Note: Also called 0-1 or binary knapsack (each item may be taken (1) or not (0)), in contrast to the fractional knapsack problem. Also called bounded knapsack (BKP) because there are a limited number of items, in contrast to the unbounded knapsack problem. The decision problem is, given items of different values and volumes and a knapsack, is there a subset that exceeds a certain value? The decision problem is NP-complete.

Author: PEB

Implementation

Steven Skiena's Stony Brook Algorithm Repository (Fortran and Pascal). GAMS Class G2c3 (Fortran).

More information

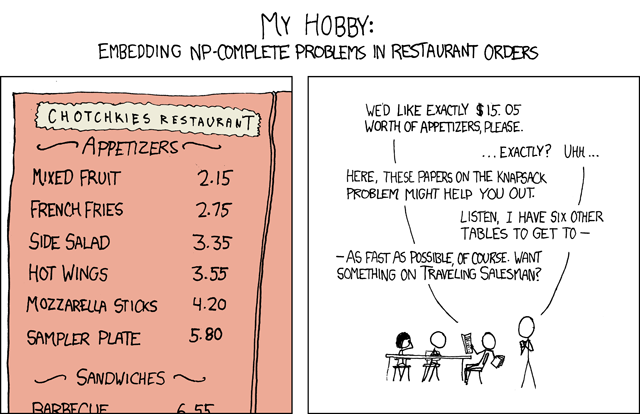
From xkcd 287 by Randall Munroe. Creative Commons Attribution-NonCommercial 2.5 License.

Go to the Dictionary of Algorithms and Data Structures home page.

If you have suggestions, corrections, or comments, please get in touch with Paul Black.

Entry modified 26 July 2021.
HTML page formatted Wed Oct 30 12:15:30 2024.

Cite this as:
Paul E. Black, "knapsack problem", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. 26 July 2021. (accessed TODAY) Available from: https://www.nist.gov/dads/HTML/knapsackProblem.html