(definition)
Definition: The dual of a planar graph, G, is a graph with a vertex for each region in G and an edge between vertices for each pair of adjacent regions. The new edge crosses the edge in G which is the boundary between the adjacent regions.
Generalization (I am a kind of ...)
planar graph.
Note:
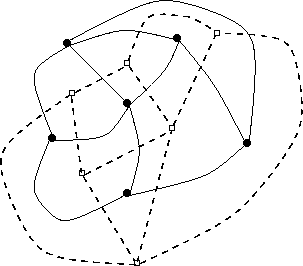
The dual of a planar graph is also planar. The original graph is the dual of the dual. That is, they are duals of each other.
In the accompanying figure, the black circles and solid lines are one planar graph. The white squares and dotted lines are another planar graph. Each is the dual of the other.
Author: PEB
If you have suggestions, corrections, or comments, please get in touch with Paul Black.
Entry modified 27 December 2010.
HTML page formatted Wed Oct 30 12:15:30 2024.
Cite this as:
Paul E. Black, "dual", in
Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. 27 December 2010. (accessed TODAY)
Available from: https://www.nist.gov/dads/HTML/dual.html