square root

(algorithm)

Definition: This describes a "long hand" or manual method of calculating or extracting square roots. Calculation of a square root by hand is a little like long-hand division.

Suppose you need to find the square root of 66564. Set up a "division" with the number under the radical. Mark off pairs of digits, starting from the decimal point and working left. (Here the decimal point is a period (.) and commas (,) mark pairs of digits.)

               ___________	
             \/  6,65,64.

Look at the leftmost digit(s) (6 in this case). What is the largest number whose square is less than or equal to it? It is 2, whose square is 4. Write 2 above, write the square below and subtract.

               __2________	
             \/  6,65,64.	
                -4		
               ----		
                 2

Now bring down the next two digits (65). The next "divisor" is double the number on top (2x2=4) and some other digit in the units position (4_).

               __2________	
             \/  6,65,64.	
                -4		
                -----		
             4_ ) 265

What is the largest number that we can put in the units and also multiply times the divisor such that the result is still be less than or equal to what we have? (Algebraically, what is d such that d × (40+d) ≤ 265?) It looks like 6 might work (since 6 × 40 = 240), but 6 is too big, since 6 × 46 = 276:

               __2__6_____	
             \/  6,65,64.	
                -4		
                -----		
             46 ) 265		
                 -276   TOO BIG

So try 5 instead.

               __2__5_____	
             \/  6,65,64.	
                -4		
                -----		
             45 ) 265		
                 -225		
                 -------		
                   40

Repeat: bring down the next two digits, and double the number on top (2 × 25 = 50) to make a "divisor", with another unit.

               __2__5_____	
             \/  6,65,64.	
                -4		
                -----		
             45 ) 265		
                 -225		
                 -------		
             50_ ) 4064

It looks like 8 would work. Let's see.

               __2__5__8__	
             \/  6,65,64.	
                -4		
                -----		
             45 ) 265		
                 -225		
                 -------		
             508 ) 4064		
                  -4064		
                  ------		
                      0

So the square root of 66564 is 258. You can continue for as many decimal places as you need: just bring down more pairs of zeros.

Here is an example spanning the decimal point. When a number does not have a rational square root, you can continue calculating (significant) digits as long as you wish.

       __1__6.8_4_0_4_2_7_5_...
     \/  2,83.6		
        -1		
        -----		
     26 ) 183		
         -156		
         ------		
     328 ) 2760		
          -2624		
          -------	
     3364 ) 13600	
           -13456	
           --------	
     33680 )  14400	
                 -0	
            ---------	
     336804 ) 1440000	
             -1347216	
             ----------	
     3368082 )  9278400	
               -6736164	
              -----------	
     33680847 ) 254223600	
               -235765929	
               ------------	
     336808545 ) 1845767100	
                -1684042725	
                -----------	
                  161724375

Why does this work?

Consider (10A + B)² = 100A² + 2 × 10AB + B² and think about finding the area of a square. Remember that 10A + B is just the numeral with B in the units place and A in the higher position. For 42, A=4 and B=2, so 10 × 4 + 2 = 42.

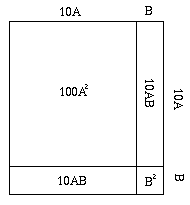
diagram of a square that is 10A + B on a side showing a 100A squared rectangle, two 10AB rectangles, and a B squared rectangle

The area of the two skinny rectangles is 2 × 10A × B. The tiny square is B². If we know A and the area of the square, S, what B should we choose?

We previously subtracted A² from S. To scale to 100A², we bring down two more digits (a factor of 100) of the size of S. We write down twice A (2A), but shifted one place to leave room for B (10 × 2A or 2 × 10A). Now we add B to get 2 × 10A + B. Multiplying by B gives us 2 × 10AB + B². When we subtract that from the remainder (remember we already subtracted A²), we have subtracted exactly (10A + B)². That is, we have improved our knowledge of the square root by one digit, B.

We take whatever remains, scale again by 100, by bringing down two more digits, and repeat the process.

See also cube root.

Note: In computers and hand-held calculators, square root, sine, cosine, and other transcendental functions are calculated with sophisticated functions, such as Taylor series, CORDIC, or Newton-Raphson method, sometimes called Newton's method.

Author: PEB

Implementation

GAMS Class C2 has many implementations of powers, roots, and reciprocals (C and Fortran). Many variations (C and Assembler) for caching, pipelined processing, etc.

More information

Another geometric justification.

Go to the Dictionary of Algorithms and Data Structures home page.

If you have suggestions, corrections, or comments, please get in touch with Paul Black.

Entry modified 6 May 2019.
HTML page formatted Mon May 6 10:22:33 2019.

Cite this as:
Paul E. Black, "square root", in Dictionary of Algorithms and Data Structures [online], Paul E. Black, ed. 6 May 2019. (accessed TODAY) Available from: https://www.nist.gov/dads/HTML/squareRoot.html